






Rules: Towers of Hanoi
1) Only one disk may be moved at time
2) May not move a larger disk on a smaller disk.
3) If more than one
disk on a tower only the smallest disk may be moved.
Table 1. Rules which must be followed to a TOH solution
Human
subjects might learn the rules by either of two methods. The first (and obvious)
method involves studying the rules as they appear in Table 1 until all three are
memorized. The more interesting method, however, involves showing the subject a
move sequence and telling her whether the move followed or broke one of the
rules. After sufficient training the subject should be able to identify a novel
move as either legal or illegal. That is the subject should, as a properly
configured neural network should, learn the TOH rules through observation.
I
recently concluded several studies in which the potential for neural nets to
recognize TOH rules was explored. My conclusions found that neural networks can,
in fact, learn TOH rules if given proper input encoding and
configuration.
Input Encoding
Twenty-seven possible legal
states exist in the standard three disk version of TOH. At time (t = 0), for
example, all three disks may rest on the left tower while at time (t = 1) both
the largest and the midsize disks may rest on the left tower with the smallest
disk resting on the right tower. The objective of the input encoding, therefore,
must be to define the state at any given time. Suppose the smallest disk were
assigned a value of 1, the midsize disk a value of 2 and the largest disk a
value of 3. Further suppose that at time (t) the largest disk is at rest on the
left tower and both the midsize and the smallest disk at rest on the middle
tower. As with this encoding scheme the numerical sum of the disks on both the
left and middle towers is 3, the precise state of the puzzle at time (t) is
ambiguous. If however the smallest disk were assigned a value of one, the
midsize disk a value of 3 and the largest disk a value of 5, the ambiguity would
no longer exist as now the left tower would hold a value of 5 (clearly the
largest disk) and the middle tower a value of 3 (clearly both the remaining
disks). Figure 1 illustrates the later encoding scheme which was adhered to
throughout this project.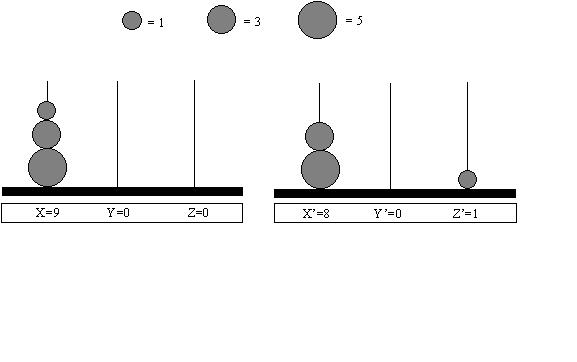
Figure 1. Input representation used throughout project TOH with
examples included to illustrate the function of the representation.
Corpus of Moves
As stated earlier there exists 27 possible legal
TOH states (shown in Figure 2). From each of these states, however, a number of
moves, both legal and illegal, may be generated. If for example one were at
state (1) at time (t = 0) the only legal moves would be to states (2) and (21).
Any other move would violate one or more rules. The complete corpus of legal and
illegal moves totals 178.
Training Set
Assembling a training
set involved pairing each of the 27 legal states with all possible legal and
illegal moves. Figure 3 illustrates a subset which has been encoded following
the scheme discussed earlier. The current state (t = 0) is state (2) from which
legal moves may be generated to states (1), (3) and (21). Moving the midsize
disk to the right tower would violate rule 2 and moving both the midsize and the
largest disks to the right tower would violate rules 1 and 2. Moving only the
largest disk to the right tower would violate rules 2 and 3.
Network
Configuration
The goal of project TOH was to discern whether a strictly
layered feed forward network could learn the rules governing a legitimate
solution to the TOH puzzle. If the network, after having been shown a sufficient
number of moves and after having been informed of the legality of each of those
moves, can correctly judge the legality of a novel move then it can be said that
the network has successfully learned the rules. The Judicial Network was
therefore configured to accept six inputs and produce one output. One input is
included for each of the three towers at time (t = 0) and one input for each of
the towers at time (t =1). The single output represents the legality of a given
move. Figure 4 illustrates an initial state (t = 0) and a next state (t = 1) as
might be perceived by a human. The states are encoded to input which are sent to
the six input units fully connected to the four hidden units. In turn the hidden
units are shown fully connected to the single output
unit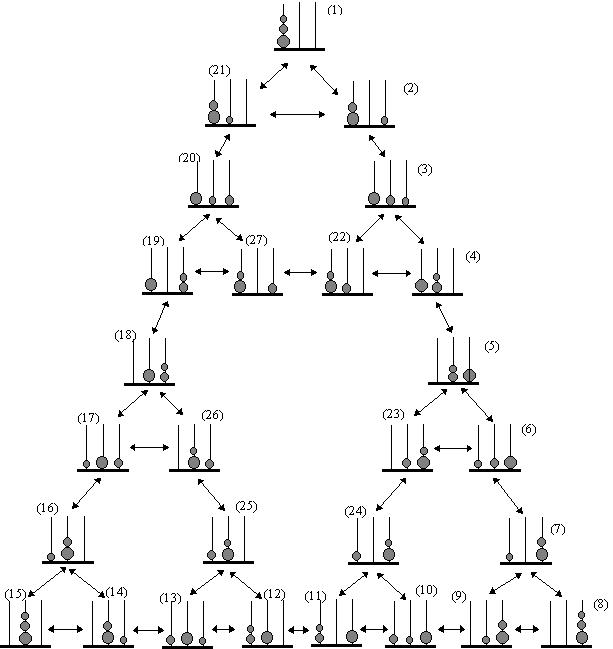
Figure 2. Illustration of all possible legal states in
TOH.

Findings and Modifications
A preliminary task of the network, as
configured above, was to simply memorize the legality of all possible moves from
two initial states (from states (2) and (3)). Though the learning rate, momentum
and number of hidden unit parameters were varied, the Total Sums Squared (tts)
error never fell below 24.0. It was assumed that the input representation was
too vague for the network to detect the relationship between the initial states,
the next states and the outputs. The input representation was therefore
modified. Each of the decimal values that had previously been encoded were
converted to binary values. As the maximum value on any tower at any given time
is nine, four binary bits were required for each decimal value. As a complete
data set contains 178 patterns each 25 bits long (including the teacher), a
program written in TURBO C was developed to convert the decimal set to binary
and write the conversions to a file using the specifications required by the
McClelland/Rumelhart Back Propagation Simulator. A sample of the data
file is shown in Figure 5. The pattern numbers are required specifications, the
first twelve bits represent the initial state, the second twelve bits represent
the next state and the last bit represents the legality of the move (1=legal).
The input modification was reflected in the configuration of the network by
expanding the number of input units to twenty-four (6x4=24). Figure 6
illustrates the modified network and is similar in format to Figure 4.
Evaluation
For purposes of training and evaluation, four
subsets of the complete 178 pattern data set were derived. The first subset
randomly deleted eighty percent of the data set leaving 35 patterns with which
to train the network and 143 (80%) novel patterns with which to evaluate the
network. The second, third and fourth subsets randomly deleted forty, sixty and
eighty percent of the data set respectively. Table 2 shows the number of
training patterns and test patterns in each of the four subsets. After training
the network on a subset until the tss fell below .04 the weights were
saved to be used in evaluation. 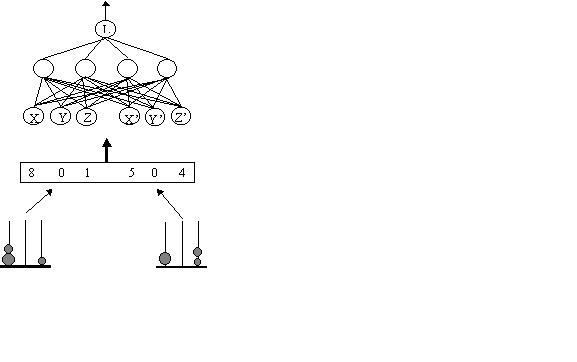
Figure 4. First Generation Judicial Network. The states are encoded
and passed to the input units which are fully connected to the hidden units. The
hidden units are in turn fully connected to the output unit.
p67
0 1 0 0 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0 0 1 0 1 1
p68 0 1 0 0 0 0 0 0 0 1 0
1 0 0 1 1 0 0 0 1 0 1 0 1 1
p70 0 1 0 0 0 0 0 0 0 1 0 1 0 1 0 0 0 1 0 1 0 0
0 0 1
p71 0 1 0 0 0 0 0 0 0 1 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0
Figure
5. Modified input representation. Pattern numbers are required, the first 12
bits represent the initial state, the second 12 bits represent the next state
and the last bit represents the legality (1 = legal).
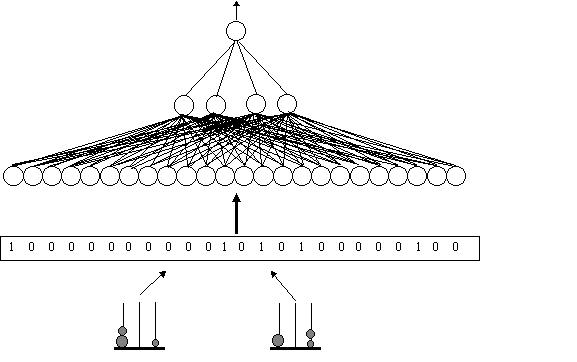
Figure 6. Second Generation Judicial Network.
no. training pats | no. test pats.
Table 2.
After the network was trained separately on each of
the four subsets the weights and corresponding test subsets were recalled and
the performance of the network was evaluated. Figure 7 indicates that when the
network was trained using only twenty percent of the data set, the correct
response to a novel pattern was produced on sixty percent of the trials. When
the network was trained on only forty percent of the data set the correct
response to a novel pattern was produced on sixty-four percent of the trials.
Trained on sixty percent of the data set, however, the network produced the
correct response on
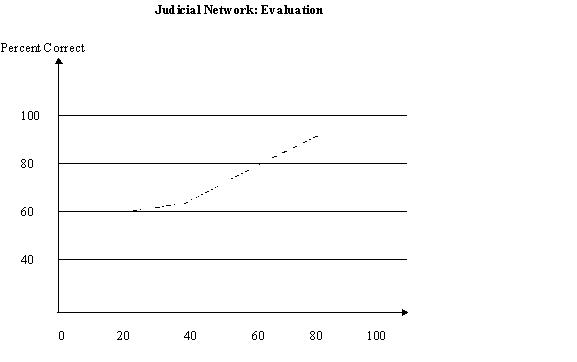
Figure 7. Performance of TOH network. Determine whether a given move
is legal.
eighty percent of the trials and on ninety-two percent of the trials when trained on eighty percent of the data set. As the probability of producing a correct output at random lies at fifty percent, that the TOH network judged the legality of a novel move at well above chance after having been trained on only twenty percent of the data set indicates that the network did, in fact, recognize the relationship between a legal and illegal move. That the TOH network's performance reached eighty percent clearly demonstrates that the TOH rules were learned by observation.
(c) Richard G. Warren - all rights reserved